Activity 13 Solution: RDDs

Activity 13 Solution: RDDs#

2025-04-08

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import statsmodels.formula.api as smf

gov_transfers = pd.read_csv("~/COMSC-341CD/data/gov_transfers.csv")

The columns we have in the dataset are:

  • \(R\) Income_Centered: the predicted income of the household, centered at 0

  • \(T\) Participation: whether the household participated in the poverty alleviation program

  • \(Y\) Support: the amount of goverment support, encoded as a survery question:

    • In relation to the previous government, do you believe that the current government is worse (0), the same (1/2), better (1)?

gov_transfers.head()
Income_Centered Participation Support
0 0.006571 0 1.0
1 0.011075 0 1.0
2 0.002424 0 1.0
3 0.007650 0 0.5
4 0.010001 0 1.0

Part 1#

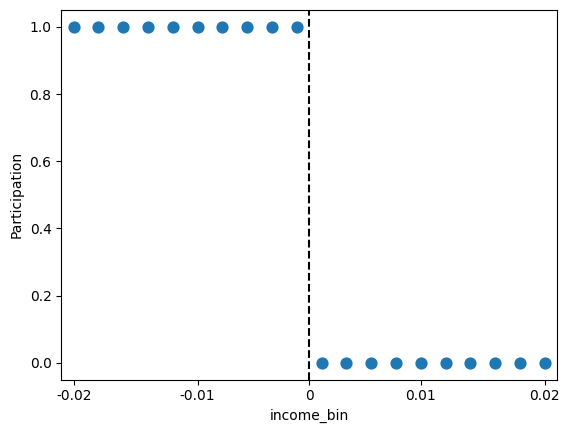
Let’s first visualize how the treatment assignment is related to the income. Use pd.cut with bins=20 and labels=False to bin the income data into 20 bins:

# TODO your code here
gov_transfers['income_bin'] = pd.cut(gov_transfers['Income_Centered'], bins=20, labels=False)
gov_transfers.head()
Income_Centered Participation Support income_bin
0 0.006571 0 1.0 13
1 0.011075 0 1.0 15
2 0.002424 0 1.0 11
3 0.007650 0 0.5 13
4 0.010001 0 1.0 15

Next, generate a sns.pointplot of y=Participation vs x=income_bin. Set linestyle='none' to plot the points individually.

Discuss with folks around you: Do you observe any deviations from the policy of assigning participation in the transfer program based on income? Does this suggest that the RDD is “sharp” or not?

Your response: pollev.com/tliu

# TODO your code here
sns.pointplot(x='income_bin', y='Participation', data=gov_transfers, linestyle='none')
# convert the xticks to the same units as the original income data
plt.xticks(ticks=[0, 5, 9.5, 14, 19], labels=[-0.02, -0.01, 0, 0.01, 0.02])
# plot the cutoff as a vertical line
plt.axvline(x=9.5, color='black', linestyle='--', label='Income cutoff')

<matplotlib.lines.Line2D at 0x329357750>
../_images/24de5c149f7820cfa1c4176e9fde4995a4a7a21be0149058a79fefbbdbf36393.png

Part 2#

Now we’ll look at the outcome variable, Support. Generate a sns.pointplot of y=Support vs x=income_bin. Set linestyle='none' to plot the points individually.

# TODO your code here
sns.pointplot(x='income_bin', y='Support', data=gov_transfers, linestyle='none')
plt.xticks(ticks=[0, 5, 9.5, 14, 19], labels=[-0.02, -0.01, 0, 0.01, 0.02])
plt.axvline(x=9.5, color='black', linestyle='--', label='Income cutoff')

<matplotlib.lines.Line2D at 0x329408f10>
../_images/6cd106896f55fca600a1add3a404117646d0d762e1bc57599b9fbaa73c06898b.png

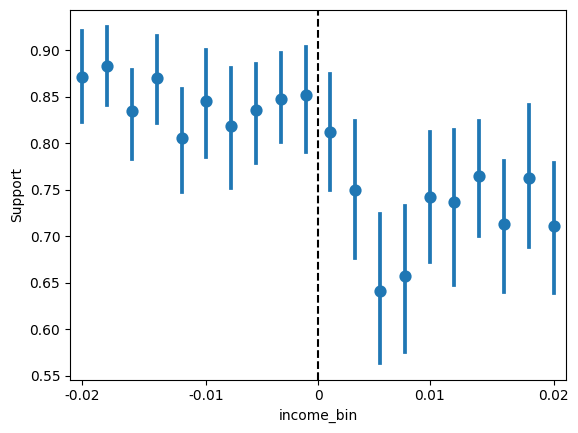
On Worksheet 5, we fit two linear regressions on either side of the cutoff. Another approach to estimating the average treatment effect is to fit a single linear regression that allows the slope to change at the cutoff:

\[ Y = \beta_0 + \beta_1 (R - c) + \beta_2 T + \beta_3 (R -c ) \cdot T \]

Since \(c=0\), this simplifies to:

\[ Y = \beta_0 + \beta_1 R + \beta_2 T + \beta_3 R\cdot T \]

The average treatment effect at the cutoff is then given by \(\beta_2\).

# TODO your code here
rdd_formula = 'Support ~ 1 + Income_Centered + Participation + Income_Centered*Participation'
rdd_model = smf.ols(rdd_formula, data=gov_transfers).fit()
print(rdd_model.params['Participation'])

0.09985188527415872

What is your estimate of the average treatment effect at the cutoff (rounded to 1 decimal place)?

Your response: pollev.com/tliu

Acknowledgements#

This activity uses data from Nick Huntington-Klein’s causaldata package.

Contents