Activity 14 Solution: Panel data#
2025-04-15
import linearmodels as lm
import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
Part 1#
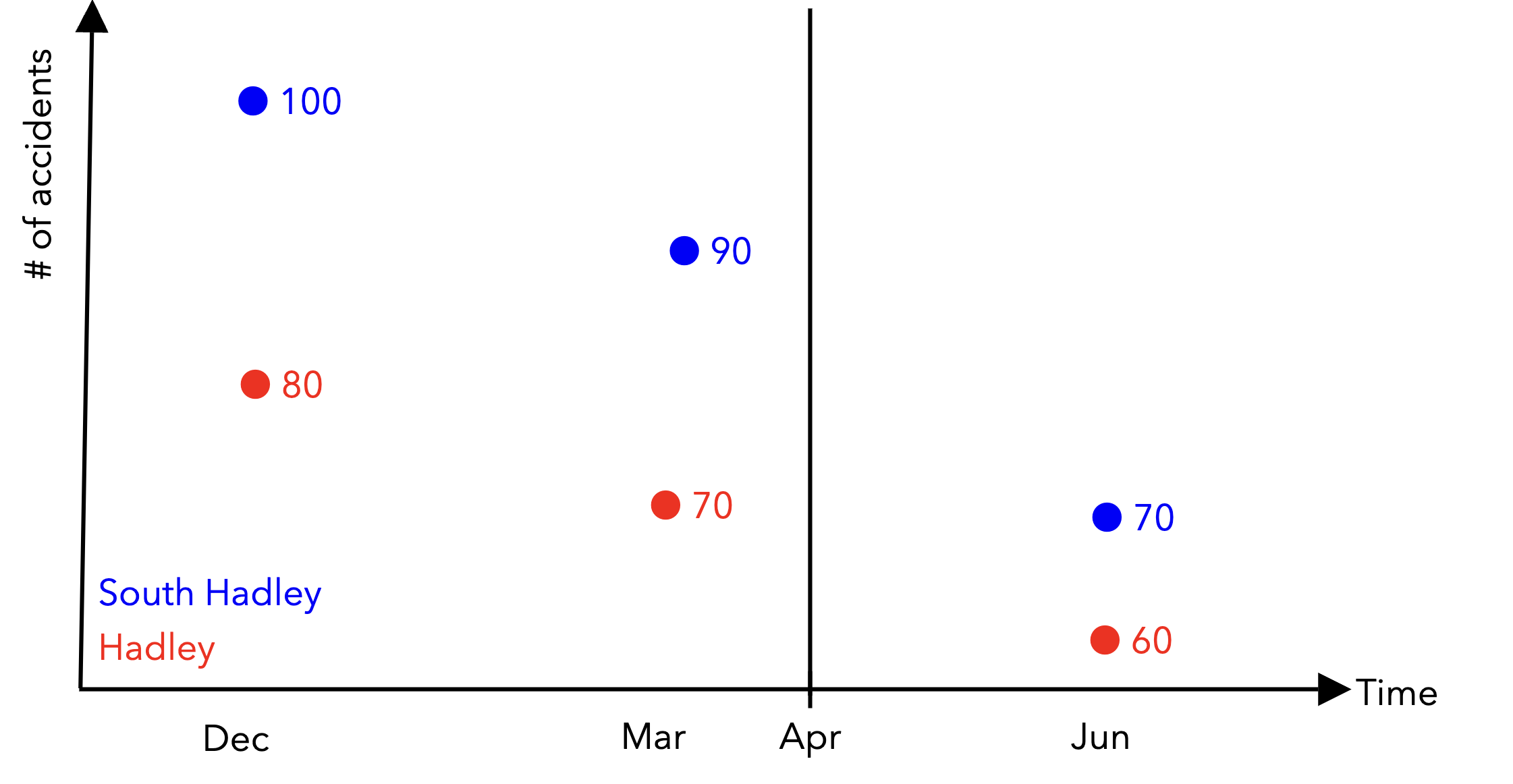
With panel data, instead of having a single row per unit in our dataframes, we have potentially multiple datapoints per unit across time. Given that:
December: \(t=1\)
March: \(t=2\)
June: \(t=3\)
We have 3 datapoints for each town. The “Post-treatment period?” column is a binary variable that is 1 if the datapoint is in the post-treatment period and 0 otherwise.
Finish populating the markdown table below with the correct values:
Unit |
Time |
Outcome |
Post-treatment period? |
|---|---|---|---|
South Hadley |
1 |
100 |
0 |
South Hadley |
2 |
90 |
0 |
South Hadley |
3 |
70 |
1 |
Hadley |
1 |
80 |
0 |
Hadley |
2 |
70 |
0 |
Hadley |
3 |
60 |
1 |
We can use pandas MultiIndex to represent the multiple indices needed for panel data. The pd.set_index() can take a list of columns to use as the new index.
traffic_df = pd.DataFrame(
{
'town': ['South Hadley', 'South Hadley', 'South Hadley', 'Hadley', 'Hadley', 'Hadley'],
'time': [1, 2, 3, 1, 2, 3],
'outcome': [100, 90, 70, 80, 70, 60],
"post_treatment": [0, 0, 1, 0, 0, 1]
}
)
# Set the index to be the['town', 'time'] columns
traffic_df = traffic_df.set_index(["town", "time"])
display(traffic_df)
# note that time and town are no longer columns
display(traffic_df.columns)
| outcome | post_treatment | ||
|---|---|---|---|
| town | time | ||
| South Hadley | 1 | 100 | 0 |
| 2 | 90 | 0 | |
| 3 | 70 | 1 | |
| Hadley | 1 | 80 | 0 |
| 2 | 70 | 0 | |
| 3 | 60 | 1 |
Index(['outcome', 'post_treatment'], dtype='object')
The multi-index is now, where the first level (level=0) is the town and the second level (level=1) is the time.
With a multi-index, the .loc method can take a tuple that specifies an index to retrieve:
# selects all the South Hadley datapoints
display(traffic_df.loc["South Hadley"])
| outcome | post_treatment | |
|---|---|---|
| time | ||
| 1 | 100 | 0 |
| 2 | 90 | 0 |
| 3 | 70 | 1 |
# selects the row for South Hadley at time 1
display(traffic_df.loc[("South Hadley", 1)])
# equivalently, we can chain the `.loc` method to filter different levels of the multi-index
display(traffic_df.loc["South Hadley"].loc[1])
outcome 100
post_treatment 0
Name: (South Hadley, 1), dtype: int64
outcome 100
post_treatment 0
Name: 1, dtype: int64
To select rows based on the second level of the multi-index, we can use pd.xs, which takes a cross-section of the DataFrame:
# Select all rows where the second level of the multi-index (time) equals 1
traffic_df.xs(1, level=1)
| outcome | post_treatment | |
|---|---|---|
| town | ||
| South Hadley | 100 | 0 |
| Hadley | 80 | 0 |
Write a line of code to select the Hadley datapoint at time 3, and submit your answer to pollEverywhere:
Part 2#
Run the cell below to load the organ donation data. The dataframe has the following columns:
State: the state name
Quarter: the quarter of data
Quarter_Num: the quarter number
Rate: the organ donation registration rate
organ_df = pd.read_csv("~/COMSC-341CD/data/organ_donations.csv")
Since the data is quarterly and begins in 2010 Q4, the first post-treatment period (after July 2011) is 2011 Q3, which corresponds to Quarter_Num = 4. Create the following columns to prepare the data for a difference-in-differences analysis:
is_california: a binary variable indicating whether the state is Californiapost_treatment: a binary variable indicating whether the quarter is after 2011 Q3 (Quarter_Num >= 4)is_treated: a binary variable indicating whether the state is California AND the quarter is after 2011 Q3
# TODO: Create the columns
organ_df['is_california'] = None
organ_df['post_treatment'] = None
organ_df['is_treated'] = None
### BEGIN SOLUTION
organ_df['is_california'] = organ_df['State'] == 'California'
organ_df['post_treatment'] = organ_df['Quarter_Num'] >= 4
organ_df['is_treated'] = organ_df['is_california'] & organ_df['post_treatment']
### END SOLUTION
Like we did in part 1, set the index to be the ['State', 'Quarter_Num'] columns.
organ_df = organ_df.set_index(['State', 'Quarter_Num'])
Finally, let’s visually evaluate the parallel trends assumption by plotting the rate against the quarter number in the pre-treatment period.
# Select the dataframe for the pre-treatment period
organ_df_pre = organ_df[organ_df['post_treatment']==False]
# Plot an sns.pointplot using organ_df_pre of 'Rate' against 'Quarter_Num', with 'is_california' as the hue
sns.pointplot(x='Quarter_Num', y='Rate', data=organ_df_pre, hue='is_california')
<Axes: xlabel='Quarter_Num', ylabel='Rate'>
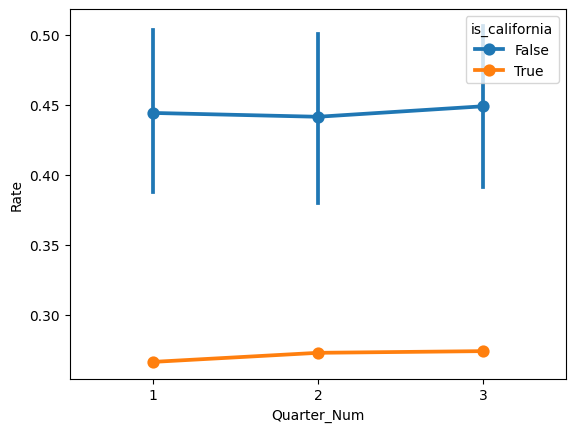
Does there appear to be any clear violations of the parallel trends assumption?
Part 3#
We just discussed the following formula for using regression to compute a difference-in-differences estimate:
Write the formula in terms of the variables in the organ_df dataframe we created in part 2. The outcome of interest is Rate, while the treated group is California.
formula = 'Rate ~ 1 + is_california + post_treatment + is_treated'
did_model = smf.ols(formula, data=organ_df)
did_results = did_model.fit()
print(did_results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: Rate R-squared: 0.054
Model: OLS Adj. R-squared: 0.036
Method: Least Squares F-statistic: 3.015
Date: Tue, 20 May 2025 Prob (F-statistic): 0.0317
Time: 10:55:06 Log-Likelihood: 78.895
No. Observations: 162 AIC: -149.8
Df Residuals: 158 BIC: -137.4
Df Model: 3
Covariance Type: nonrobust
==========================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------------
Intercept 0.4449 0.017 26.101 0.000 0.411 0.479
is_california[T.True] -0.1736 0.089 -1.960 0.052 -0.349 0.001
post_treatment[T.True] 0.0139 0.024 0.578 0.564 -0.034 0.062
is_treated[T.True] -0.0225 0.125 -0.179 0.858 -0.270 0.225
==============================================================================
Omnibus: 0.962 Durbin-Watson: 0.309
Prob(Omnibus): 0.618 Jarque-Bera (JB): 1.035
Skew: -0.106 Prob(JB): 0.596
Kurtosis: 2.670 Cond. No. 13.9
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
What is your ATT estimate of the effect of active choice vs opt-in on California organ donation rates?
Acknowledgements#
This activity is derived from Nick Huntington-Klein’s analysis of Kessler and Roth (2014) in Chapter 18 of The Effect.
