Activity 17: Panel data Solutions

Activity 17: Panel data Solutions#

import seaborn as sns
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf

Part 1#

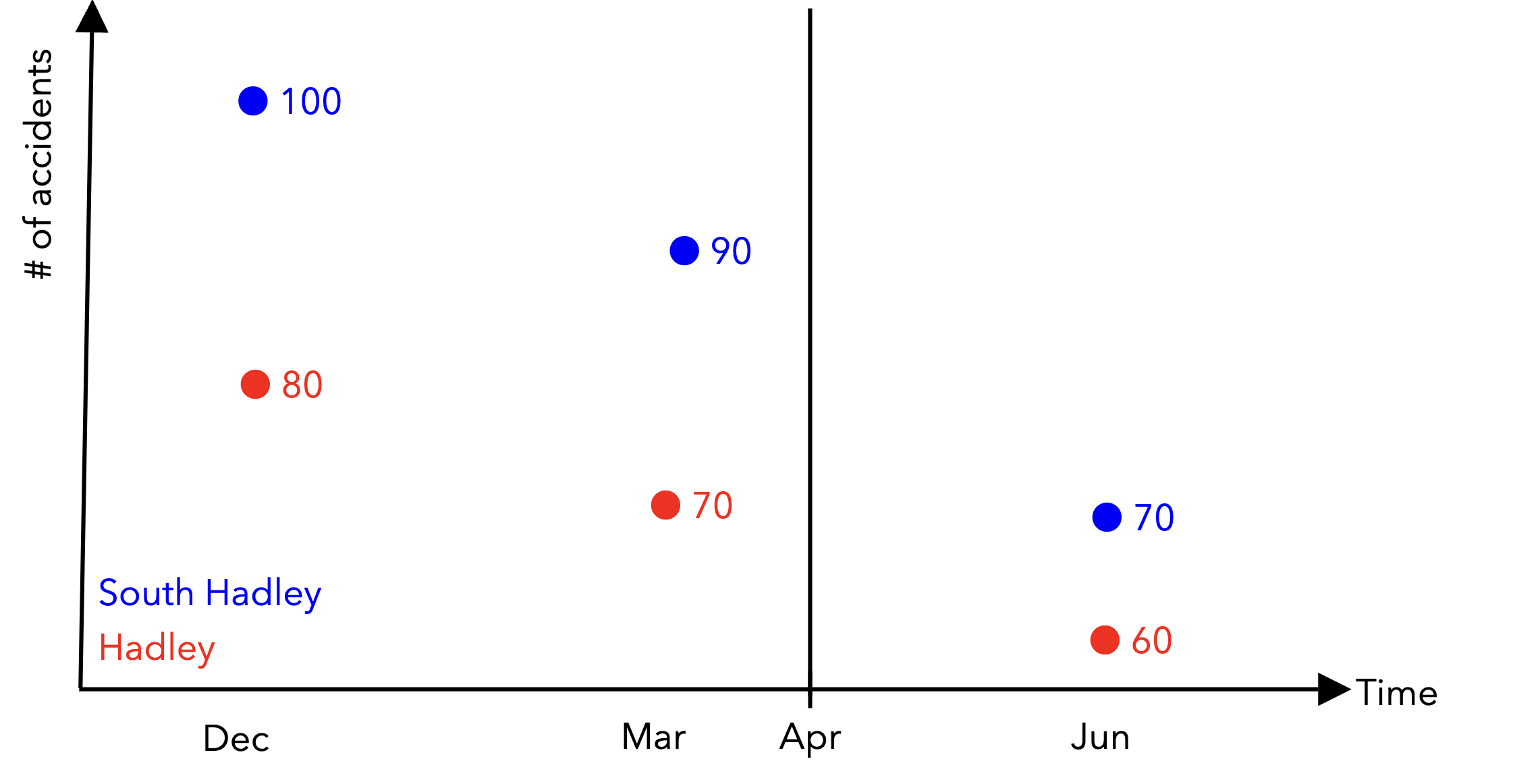
With panel data, instead of having a single row per unit in our dataframes, we have potentially multiple datapoints per unit across time. Given that:

  • December: \(t=1\)

  • March: \(t=2\)

  • June: \(t=3\)

We have 3 datapoints for each town. The “Post-treatment period?” column is a binary variable that is 1 if the datapoint is in the post-treatment period and 0 otherwise.

Finish populating the markdown table below with the correct values:

Unit

Time

Outcome

Post-treatment period?

South Hadley

1

100

0

South Hadley

2

90

0

South Hadley

3

70

1

Hadley

1

80

0

Hadley

2

70

0

Hadley

3

60

1

We can use pandas MultiIndex to represent the multiple indices needed for panel data. The pd.set_index() can take a list of columns to use as the new index.

traffic_df = pd.DataFrame(
    {
        'town': ['South Hadley', 'South Hadley', 'South Hadley', 'Hadley', 'Hadley', 'Hadley'],
        'time': [1, 2, 3, 1, 2, 3],
        'outcome': [100, 90, 70, 80, 70, 60],
        "post_treatment": [0, 0, 1, 0, 0, 1]
    }
)

# TODO set the index to be the['town', 'time'] columns
traffic_df = traffic_df.set_index(["town", "time"])

display(traffic_df)

# note that time and town are no longer columns
display(traffic_df.columns)
outcome post_treatment
town time
South Hadley 1 100 0
2 90 0
3 70 1
Hadley 1 80 0
2 70 0
3 60 1 
Index(['outcome', 'post_treatment'], dtype='object')

The multi-index is now, where the first level (level=0) is the town and the second level (level=1) is the time.

With a multi-index, the .loc method can take a tuple that specifies an index to retrieve:

# selects all the South Hadley datapoints
display(traffic_df.loc["South Hadley"])
outcome post_treatment
time
1 100 0
2 90 0
3 70 1 
# selects the row for South Hadley at time 1
display(traffic_df.loc[("South Hadley", 1)])
#display(traffic_df.loc[("South Hadley", 1)])

# equivalently, we can chain the `.loc` method to filter different levels of the multi-index
display(traffic_df.loc["South Hadley"].loc[1])
#display(traffic_df.loc["South Hadley"].loc[1])

outcome           100
post_treatment      0
Name: (South Hadley, 1), dtype: int64

outcome           100
post_treatment      0
Name: 1, dtype: int64

To select rows based on the second level of the multi-index, we can use pd.xs, which takes a cross-section of the DataFrame:

# Select all rows where the second level of the multi-index (time) equals 1
traffic_df.xs(1, level=1)
outcome post_treatment
town
South Hadley 100 0
Hadley 80 0

Write a line of code to select the Hadley datapoint at time 3, and submit your answer to pollEverywhere:

display(traffic_df.loc[("Hadley", 3)])

outcome           60
post_treatment     1
Name: (Hadley, 3), dtype: int64

Part 2#

Run the cell below to load the organ donation data. The dataframe has the following columns:

  • State: the state name

  • Quarter: the quarter of data

  • Quarter_Num: the quarter number

  • Rate: the organ donation registration rate

organ_df = pd.read_csv("~/COMSC-341CD/data/organ_donations.csv")

organ_df.head(10)
State Quarter Rate Quarter_Num
0 Alaska Q42010 0.7500 1
1 Alaska Q12011 0.7700 2
2 Alaska Q22011 0.7700 3
3 Alaska Q32011 0.7800 4
4 Alaska Q42011 0.7800 5
5 Alaska Q12012 0.7900 6
6 Arizona Q42010 0.2634 1
7 Arizona Q12011 0.2092 2
8 Arizona Q22011 0.2261 3
9 Arizona Q32011 0.2503 4

Since the data is quarterly and begins in 2010 Q4, the first post-treatment period (after July 2011) is 2011 Q3, which corresponds to Quarter_Num = 4. Create the following columns to prepare the data for a difference-in-differences analysis:

  • is_california: a binary variable indicating whether the state is California

  • post_treatment: a binary variable indicating whether the quarter is after 2011 Q3 (Quarter_Num >= 4)

  • is_treated: a binary variable indicating whether the state is California AND the quarter is after 2011 Q3

#organ_df[['State', 'is_california']].head(20)

# TODO: Create the columns
organ_df['is_california'] = organ_df.loc[:, 'State'] == 'California'
organ_df['post_treatment'] = organ_df['Quarter_Num'] >= 4
organ_df['is_treated'] = organ_df['is_california'] & organ_df['post_treatment']

organ_df[['Quarter_Num', 'post_treatment', 'State', 'is_treated']].head(20)
Quarter_Num post_treatment State is_treated
0 1 False Alaska False
1 2 False Alaska False
2 3 False Alaska False
3 4 True Alaska False
4 5 True Alaska False
5 6 True Alaska False
6 1 False Arizona False
7 2 False Arizona False
8 3 False Arizona False
9 4 True Arizona False
10 5 True Arizona False
11 6 True Arizona False
12 1 False California False
13 2 False California False
14 3 False California False
15 4 True California True
16 5 True California True
17 6 True California True
18 1 False Colorado False
19 2 False Colorado False

Like we did in part 1, set the index to be the ['State', 'Quarter_Num'] columns.

# TODO set the multi-index
#organ_df.set_index(TODO)

Finally, let’s visually evaluate the parallel trends assumption by plotting the rate against the quarter number in the pre-treatment period.

# TODO select the dataframe for the pre-treatment period
organ_df_pre = None


# TODO plot an sns.pointplot using organ_df_pre of 'Rate' against 'Quarter_Num', with 'is_california' as the hue
# sns.pointplot()

Does there appear to be any clear violations of the parallel trends assumption?

Part 3#

We just discussed the following formula for using regression to compute a difference-in-differences estimate:

\[ Y = \beta_0 + \beta_1 (\text{treated group}) + \beta_2 (\text{after treatment}) + \beta_3 (\text{treated group} \times \text{after treatment}) + \epsilon \]

Write the formula in terms of the variables in the organ_df dataframe we created in part 2. The outcome of interest is Rate, while the treated group is California.

# TODO your code here
formula = ''

# did_model = smf.ols(TODO)
# did_results = did_model.fit()
# print(did_results.params)

What is your ATT estimate of the effect of active choice vs opt-in on California organ donation rates?

Acknowledgements#

This activity is derived from Nick Huntington-Klein’s analysis of Kessler and Roth (2014) in Chapter 18 of The Effect.

Contents